問題
May Leetcoding Challange Complementの15日目です。 あっという間に5月の半ばです。
この問題は「Kadane's Algorithm」の応用問題です。
Kadane's Algrorithmとは
以下のようなマイナスを含むArrayの連続したSubarrayの最大和を求めるアルゴリズムです。
[-1, 3, 4, -10, 8] => この場合、[8] が部分和8が最大 [-1, 3, 4, -2, 8] => この場合、[3, 4, -2, 8]で部分和13が最大
Kadane's Algorithmとはこの問題を動的計画法で解く問題です。
以下の漸化式を立てれば、答えが導き出せます。
対象のArrayをnumとする。numのi番目の数字をnum[i]とする。 dp[i] = max(dp[i-1] + num[i], num[i])
この数式はどういう意味かというと、num を一番目から順番に足し合わせていって、足し合わせるたびに以下の2つの選択肢を考えます。
- 前からの和を引きつぐか
dp[i-1] + num[i] - 前からの和を捨てて、自分の数から仕切り直すか
num[i]
マイナスの数が多すぎて、今までの和があまりに小さい場合、仕切り直したほうが和が大きくなる場合があります。
以下のような例です。(いつものようにクソ雑な図。今回からタブレットを使ってみました。)
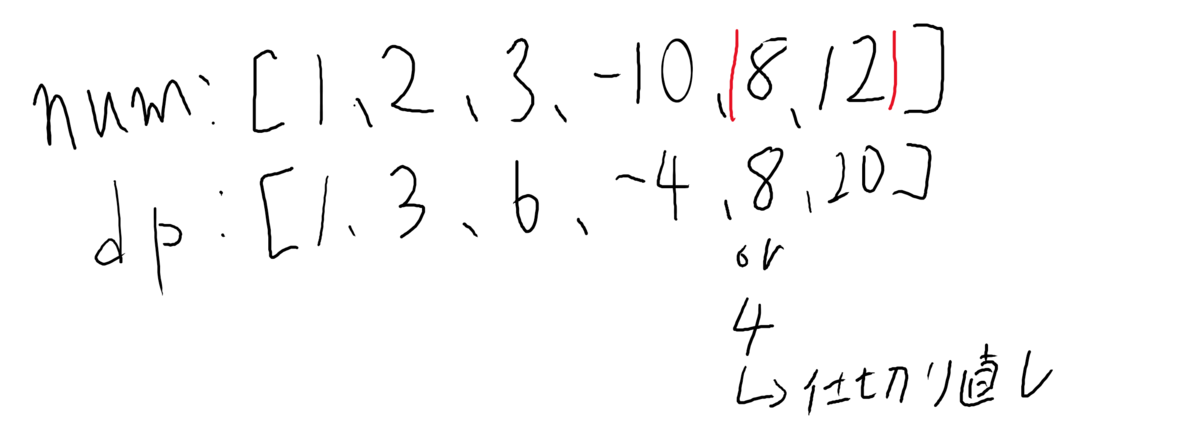
これをコードに起こすと以下の形になります。
def kadane(nums): dp = [0] * len(nums) dp[0] = nums[0] for i in range(1, len(nums)): dp[i] = max(dp[i-1] + nums[i], nums[i]) return dp[-1]
これだと 空間計算量が O(n) です。
実際に必要なのは dp[i-1] だけなので、これのみを持つ変数をループごとに更新していけば O(1)で済みます。
def kadane(nums): dp = nums[0] maxSum = nums[0] for i in range(1, len(nums)): dp = max(dp + nums[i], nums[i]) maxSum = max(maxSum, dp) return maxSum
解き方
先ほども説明した通り、この問題はこの Kadane's Algorithmの応用です。
ただし問題となる配列が循環する配列のため、以下の2パターンに分けて考える必要があります。
- 部分和が一つの配列内で完結するパターン 例: [[3,-2,2],-3] => [3,-2,2] が部分和
- 部分和が配列を跨ぐパターン 例: [5,-3,5] => [5, -3, 5] が部分和
この1のパターンは、普通にKadane's Algorithmで求めることができます。 2のパターンをどうやって出すか?がこの問題の鬼門です。
2パターンを考えると、以下の図のように、全体から真ん中の配列だけ差し引けばよいことがわかります。

この差し引く配列の数が小さい=マイナスをかけて、最大のもの部分長配列を求める問題、と言い換えることができます。
ただし、すべての配列を選んでしまうと、空の配列を選ぶことになってしまうため、最初と最後の数をそれぞれ除いた2パターンでKadane's Algroithmを行います。
回答
class Solution: def maxSubarraySumCircular(self, A: List[int]) -> int: def kadane(nums: List[int]): if not nums: return 0 dp = nums[0] maxSum = nums[0] for i in range(1, len(nums)): dp = max(dp + nums[i], nums[i]) maxSum = max(maxSum, dp) return maxSum maxSum = kadane(A) maxSum1 = sum(A) + kadane([-1 * A[i] for i in range(1, len(A))]) maxSum2 = sum(A) + kadane([-1 * A[i] for i in range(0, len(A)-1)]) return max(maxSum, maxSum1, maxSum2)
計算量
時間計算量: O(N)
空間計算量: O(1)